4  Престратификация

Материал написан на основе статьи Xie, H., & Aurisset, J. (2016, August). Improving the sensitivity of online controlled experiments: Case studies at netflix. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 645-654).

4.1 Стратификация (stratification sampling)

Мы помним, что снижение дисперсии снижает необходимое число наблюдений.

Предположим, что мы выбрали переменную, по которой мы можем разбить нашу выборку на группы (страты). Пусть таких групп K штук, а \(n_k\) – численность каждой из них, то есть \(\displaystyle{\sum_{k=1}^K n_k = N}\), где \(N\) величина генеральной совокупности. Тогда вероятность попасть в одну из групп равняется \(p_k = \frac{n_k}{N}\) – доля людей из \(k\)-й страты в генеральной совокупности.

Пусть наша зависимая переменная равна \(Y\), причем \(\mathbb{E}(Y)=\mu\) и \(var(Y)=\sigma^2\). Тогда среднее значение зависимой переменной равно:

• Обычное среднее по всей выборке:\(\displaystyle{\bar{Y}=\frac{1}{N} \sum_{k=1}^K \sum_{j=1}^{n_k} Y_{kj}}\)

• Средневзвешенное при стратификации равно сумме средних в каждой страте, взвешенных по вероятностям попасть в каждую из этих страт: \(\displaystyle{\hat{Y}_{\text{strat}}=\sum_{k=1}^K p_k \bar{Y}_k}\), где \(\displaystyle{\bar{Y}_k=\frac{1}{n_k} \sum_{j=1}^{n_k} Y_{kj}}\) среднее значение метрики внутри \(k\)-й страты.

Распишем среднее при стратификации подробнее:

\(\displaystyle{\underbrace{\sum_{k=1}^K p_k \bar{Y}_k}_{\hat{Y}_{\text{strat}}} = \sum_{k=1}^K \frac{n_k}{N} \frac{1}{n_k} \sum_{j=1}^{n_k} Y_{kj} = \underbrace{\frac{1}{N} \sum_{k=1}^K \sum_{j=1}^{n_k} Y_{kj}}_{\bar{Y}}}\) обе средние равны.

Найдем среднее и дисперсию зависимой переменной при стратификации.

• Среднее: \(\displaystyle{\mathbb{E}\left(\hat{Y}_{\text{strat }}\right)=\mathbb{E}\left[\sum_{k=1}^K p_k \bar{Y}_k\right]=\sum_{k=1}^K p_k \mathbb{E}\left(\bar{Y}_k\right)=\sum_{k=1}^K p_k \mu_k=\boxed{\mu}}\)
• Дисперсия: \(\displaystyle{var\left(\hat{Y}_{\text{strat }}\right)=\operatorname{var}\left[\sum_{k=1}^K p_k \bar{Y}_k\right]=\sum_{k=1}^K p_k^2 var\left(\bar{Y}_k\right)=\sum_{k=1}^K \frac{n_k^2}{N^2} \frac{1}{n_k^2} n_k \sigma_k^2 = \frac{1}{N} \sum_{k=1}^K \frac{n_k}{N} \sigma_k^2 = \boxed{\frac{1}{N} \sum_{k=1}^K p_k \sigma_k^2}}\)(1)

4.2 Простая рандомизация (simple random sampling)

Аналогично найдем среднее и дисперсию зависимой переменной при классическом эксперименте.

• Среднее: \(\displaystyle{\mathbb{E}(\bar{Y})=\mathbb{E}\left[\frac{1}{N} \sum_{k=1}^K \sum_{j=1}^{n_k} Y_{k j}\right]=\frac{1}{N} \sum_{k=1}^K \sum_{j=1}^{n_k} \mathbb{E}\left(Y_{k j}\right)=\frac{1}{N} \sum_{k=1}^K \sum_{j=1}^{n_k} \mu = \frac{1}{N} \sum_{k=1}^K n_k \mu = \frac{1}{N} N \mu=\boxed{\mu}}\)
• Дисперсия: \(\displaystyle{\operatorname{var}(\bar{Y})=var\left[\frac{1}{N} \sum_{k=1}^K \sum_{j=1}^{n_k} Y_{kj}\right]= \frac{1}{N^2} \sum_{k=1}^K \sum_{j=1}^{n_k} var\left(Y_{kj}\right) = \frac{1}{N^2} \sum_{k=1}^K n_k \sigma^2 = \frac{N \sigma^2}{N^2}=\boxed{\frac{\sigma^2}{N}}}\)(2)

4.3 Total variance law

Дисперсия зависимой переменной при рандомизированном эксперименте может быть представлена в виде суммы внутригрупповой и межгрупповой дисперсии.

Для этого нам понадобится total variance law (см. доказательство в приложении): \(\displaystyle{var(Y)=var[\mathbb{E}(Y \mid X)] + \mathbb{E}[var(Y\mid X)]}\)

Пусть \(Z\) – номер страты от 1 до K, тогда: \(\displaystyle{var(Y)=\mathbb{E}(var(Y \mid Z))+var(\mathbb{E}(Y \mid Z))=}\)

\(\displaystyle{=\left\{ I(Z = k) \text{ индикаторная переменная, равная 1, если $Z = k$, и равная нулю иначе} \right\}= }\)

\(\displaystyle{=\mathbb{E}\left[\sum_{k=1}^K \sigma_k^2 I(Z=k)\right]+ var\left[\sum_{k=1}^K \mu_k I(Z=k)\right]=}\)

\(\displaystyle{=\sum_{k=1}^K \sigma_k^2 \mathbb{E}[I(Z=k)]+\mathbb{E}\left[\sum_{k=1}^K \mu_k I(Z=k)\right]^2-\left[\mathbb{E}\left[\sum_{k=1}^K \mu_k I(Z=k)\right]\right]^2=}\)

\(\displaystyle{= \sum_{k=1}^K \sigma_k^2 p_k + \sum_{k=1}^K \mu_k^2 p_k - \mu^2 = \{*\} = \sum_{k=1}^K \sigma_k^2 p_k + \sum_{k=1}^K p_k (\mu_k - \mu)^2}\) (3)

\(\displaystyle{(*): \sum_{k=1}^K p_k(\mu_k - \mu)^2 = \sum_{k=1}^K p_k\left(\mu_k^2 - 2\mu\mu_k + \mu^2\right) =}\)

\(\displaystyle{= \sum_{k=1}^K p_k \mu_k^2 - 2\mu \sum_{k=1}^K \mu_k p_k+ \mu^2 \sum_{k=1}^K p_k = \sum_{k=1}^K \mu_k^2 p_k - 2\mu^2 + \mu^2 =\sum_{k=1}^K \mu_k^2 p_k - \mu^2}\)

Из (2) и (3) следует:

\(\displaystyle{var(\bar{Y})=\frac{\sigma^2}{N}}\)

\(\displaystyle{var(Y)=\sum_{k=1}^K \sigma_k^2 p_k+\sum_{k=1}^K p_k\left(\mu_k-\mu\right)^2}\)

\(\displaystyle{var(\bar{Y})= \underbrace{\frac{1}{N} \sum_{k=1}^K p_k \sigma_k^2}_{\text{внутригрупповая дисперсия}} + \underbrace{\frac{1}{N} \sum_{k=1}^K p_k \left(\mu_k-\mu\right)^2}_{\text{межгрупповая дисперсия}}}\) (4)

Из (1) и (4) следует:

\(\displaystyle{var\left(\hat{Y}_{\text{strat}}\right) = \frac{1}{N} \sum_{k=1}^K p_k \sigma_k^2}\)

\(\displaystyle{var(\bar{Y})= \underbrace{\frac{1}{N} \sum_{k=1}^K p_k \sigma_k^2}_{\text{внутригрупповая дисперсия}} + \underbrace{\frac{1}{N} \sum_{k=1}^K p_k \left(\mu_k-\mu\right)^2}_{\text{межгрупповая дисперсия}}}\)

Дисперсия среднего значения зависимой переменной всегда больше, чем дисперсия среднего значения зависимой переменной в случае стратификации, поскольку межгрупповая дисперсия всегда неотрицательная. Таким образом, \(\displaystyle{var(\bar{Y}) \geqslant var\left(\hat{Y}_{\text{strat }}\right)}\)

4.4 Приложение

4.4.1 Условные обозначения

• \(Y\) – зависимая переменная, причем
  • \(\mathbb{E}(Y)=\mu\)
  • \(var(y)=\sigma^2\)
• Выборка разбита на \(k\) страт по показателю \(X\), то есть
  • \(\mu_k\) – среднее в страте
  • \(\sigma^2_k\) – дисперсия в страте
  • \(n_k\) – численность в страты, то есть \(\sum_{k=1}^K n_k = N\)
  • \(p_k = \frac{n_k}{N}\) – доля людей из \(k\)-й страты в генеральной совокупности
  • \(Y_{kj}\) – метрика \(j\)-го человека из \(k\)-й страты
• Тогда среднее значение зависимой переменной
  • \(\displaystyle{\bar{Y}=\frac{1}{N} \sum_{k=1}^K \sum_{j=1}^{n_k} Y_{kj}}\) обычное среднее
  • \(\displaystyle{\hat{Y}_{\text{strat}}=\sum_{k=1}^K p_k \bar{Y}_k}\) среднее при стратификации
    • \(\displaystyle{\bar{Y}_k=\frac{1}{n_k} \sum_{j=1}^{n_k} Y_{kj}}\) среднее значение метрики внутри \(k\)-й страты
  • \(\displaystyle{\underbrace{\sum_{k=1}^K p_k \bar{Y}_k}_{\hat{Y}_{\text{strat}}} = \sum_{k=1}^K \frac{n_k}{N} \frac{1}{n_k} \sum_{j=1}^{n_k} Y_{kj} = \underbrace{\frac{1}{N} \sum_{k=1}^K \sum_{j=1}^{n_k} Y_{kj}}_{\bar{Y}}}\) обе средние равны

4.4.2 Total variance law

Это вспомогательный факт из математической статистики, который нам понадобится в дальнейших выкладках.

Доказать:

\(\displaystyle{var(Y)=var_X(\mathbb{E}(Y \mid X)) + \mathbb{E}_X(var(yX\mid X))}\)

Доказательство:

\(\displaystyle{var(Y)=\mathbb{E}\left(Y^2\right)-(E(Y))^2 =}\)

\(\displaystyle{= \left\{\text{закон повтороного мат. ожидания } \mathbb{E}(Y) = \mathbb{E}(\mathbb{E}(Y \mid X))\right\} =}\)

\(\displaystyle{=\mathbb{E}\left(\mathbb{E}\left(Y^2 \mid X\right)\right)-\mathbb{E}(\mathbb{E}(Y \mid X))]^2=}\)

\(\displaystyle{=\left\{\text{добавим и вычтем } \mathbb{E}\left[(\mathbb{E}(Y \mid X))^2 \mid X\right] \right\} =}\)

\(\displaystyle{=\underbrace{\mathbb{E}\left[\mathbb{E}\left(Y^2 \mid X\right)-(\mathbb{E}(Y \mid X))^2 \mid X\right]}_{\mathbb{E}[var(Y \mid X)]}+\underbrace{ \mathbb{E}\left[(\mathbb{E}(Y \mid X))^2 \mid X\right]-\mathbb{E}[\mathbb{E}(Y \mid X)] \mathbb{E}[\mathbb{E}(Y \mid X)]}_{var[\mathbb{E}(Y \mid X)]}=}\)

\(\displaystyle{=\mathbb{E}[\operatorname{var}(Y \mid X)]+\operatorname{var}[\mathbb{E}(Y \mid X)]}\)

4.5 Симуляция

В данной симуляции мы попробуем эмпирически доказать, что дисперсия оценки, полученной с помощью престратификации, действительно меньше, чем при оценивании с обычной рандомизацией. Чтобы получить распределение оценок, нам нужно осуществить множество реализаций нашего эксперимента. Для этого мы воспользуемся циклами.

library('dplyr')

Для начала мы заготовим несколько функций, которые мы далее сможем использовать, чтобы наш код был более компактный. Функция generate_data будет генерить нам набор данных размером N наблюдений с параметрами ниже:

generate_data <- function(N){
  N <- N
  X <- runif(N, 5, 28)
  e <- rnorm(N, 0, 1)
  number <- 1:N
  Y0 <- 10 + X + e
  Y1 <- Y0 + 7
  data <- data.frame(number=number, X=X, Y0=Y0, Y1=Y1)
  return(data)
}

Функция basic_experiment, ссылаясь на функцию generate_data, создает набор данных размером rows наблюдений, проводит на этих данных рандомизацию и считает эффект:

basic_experiment <- function(rows){
  data <- generate_data(N=rows)
  data$T <- rbinom(rows, 1, 0.5)
  data$Y <- data$T*data$Y1 + (1-data$T)*data$Y0
  mod <- lm(Y~T, data)
  ATE <- summary(mod)$coefficients[2]
  return(ATE)
}

Функция stratification_experiment, ссылаясь на функцию generate_data, создает набор данных размером rows наблюдений, затем разбивает его на страты и внутри каждой страты проводит рандомизацию, после чего считает эффект воздействия:

stratification_experiment <- function(rows){
  data <- generate_data(rows)
  data <- data[order(data$X),]
  trashhold <- quantile(data$X)
  data$group <- cut(data$X, breaks = trashhold, 
                    include.lowest = TRUE, labels = c(1:4))
  data <- data %>% 
    group_by(group) %>% 
    mutate(1:length(X) %in% sample.int(length(X), length(X)/2))
  colnames(data)[6] <- 'T'
  data$T <- as.numeric(data$T)
  data$Y <- data$T*data$Y1 + (1-data$T)*data$Y0
  mod <- lm(Y~T, data)
  ATE <- summary(mod)$coefficients[2]
  return(ATE)
}

Функция stratification_experiment в зависимости от аргумента type проводит симуляцию либо со стратификацией (type='strata'), либо без нее (type='basic'). Внутри каждой “ветки” с условием реализуется цикл, который N раз проводит эксперимент с помощью функции, которую мы написали ранее – basic_experiment или stratification_experiment. Каждый раз результаты эксперимента (оценка эффекта) сохраняется в вектор ATEs.

simulation <- function(N, rows, type){
  if (type =='basic'){
    ATEs <- c()
    i=1
    while (i<N+1) {
      ATE <- basic_experiment(rows)
      ATEs <- c(ATEs, ATE)
      i=i+1
    } 
  } else if (type =='strata'){
    ATEs <- c()
    i=1
    while (i<N+1) {
      ATE <- stratification_experiment(rows)
      ATEs <- c(ATEs, ATE)
      i=i+1
    }
  }
  return(ATEs)
}

Используя функцию simulation, проводим симуляцию N=10000 раз, каждый раз создавая набор данных из rows=1000 со стратификацией (type='strata') и без нее (type='basic').

stratification_ATEs <- simulation(N=10000, rows=1000, type='strata')
basic_ATEs <- simulation(N=10000, rows=1000, type='basic')

Построим гистограму, которая покажет нам, как распределены оценки эффекта в зависимости от способа рандомизации.

hist(basic_ATEs, col=rgb(1, 0, 0, 0.5), freq=T)
hist(stratification_ATEs, col=rgb(0, 0, 1, 0.5), freq=T, add=T)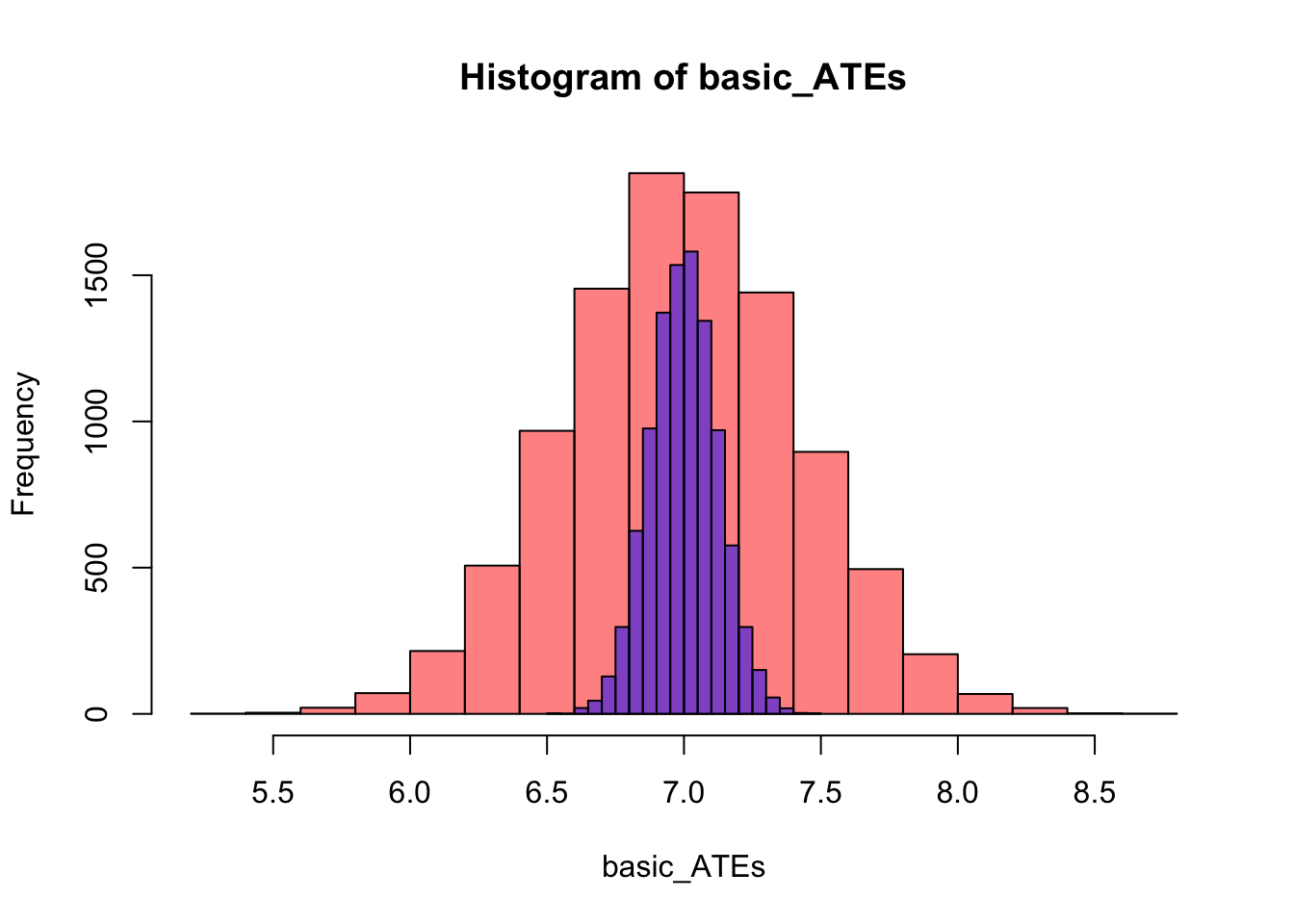

Наш теоретический вывод подтвердился. Действительно, дисперсия оценки, когда мы используем престратификацию, ниже, чем у обычной рандомизации.